In a previous post, we introduced the basic terminology of hypothesis testing. We also wanted to test the null hypothesis ![]() that the two websites have the same clickthrough rate i.e.
that the two websites have the same clickthrough rate i.e. ![]() against the alternative hypothesis
against the alternative hypothesis ![]() that
that ![]() . Here we show how to do it.
. Here we show how to do it.
Test Statistic and the t-test
A test statistic is some function of a sample that is used for hypothesis testing. The name of the test denotes the distribution of the test statistic: for instance, a z-test refers to a hypothesis test where the test statistic under the null hypothesis is Gaussian distributed. However, to use an exact z-test, we require the standard deviation of our data to be known. An alternative related test is the t-test. Consider the case of iid observations ![]() with sample mean
with sample mean ![]() for some unknown parameters
for some unknown parameters ![]() . Let
. Let ![]() which is an unbiased estimate of the variance. Then
which is an unbiased estimate of the variance. Then
(1) ![]()
has a Student’s t-distribution with ![]() degrees of freedom.
degrees of freedom.
If we wanted to test whether the population or true mean was ![]() , we would set a threshold for the p-value, for instance 0.05, let
, we would set a threshold for the p-value, for instance 0.05, let ![]() be
be ![]() -distributed with
-distributed with ![]() degrees of freedom, and then calculate whether
degrees of freedom, and then calculate whether
(2) 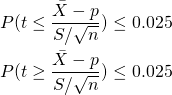
If one of these holds, then we reject the null hypothesis.
Two Samples
In our setting we don’t want to test whether our sample mean matches some hypothesized true mean, but instead want to test whether the true means between two samples are equal. That is, we have two samples ![]() with mean
with mean ![]() and
and ![]() with mean
with mean ![]() , and we assume the sample means
, and we assume the sample means ![]() and
and ![]() . Then
. Then ![]() is the sample mean of the differences. If
is the sample mean of the differences. If ![]() is the unbiased estimator of the variance of
is the unbiased estimator of the variance of ![]() and
and ![]() that for
that for ![]() , then under the null hypothesis
, then under the null hypothesis ![]() ,
, ![]() , so that
, so that
(3) 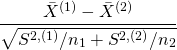
follows a student’s t-distribution with ![]() degrees of freedom.
degrees of freedom.