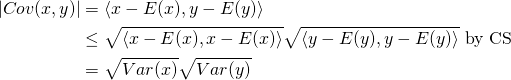The Probabilistic Cauchy Schwartz and the Analysis Cauchy Schwartz.

I’d often seen two different versions of Cauchy Schwartz (CS). In analysis and linear algebra I’d learned that if $x,y$ are elements of a vector space $V$ we have

(1) $\begin{align*} \vert \left<x,y\right>\vert &\leq \Vert x\Vert \cdot \Vert y\Vert \end{align*}$

while in probability and statistics I’d learned that for random variables $x,y$ we have

(2) $\begin{align*} \vert E(xy)\vert &\leq \sqrt{E(x^2)}\sqrt{E(y^2)} \end{align*}$

I’d seen proofs of both but not in a way that tied them together. Today, I learned how they’re related and it’s super simple. Define $\left<x,y\right>=E(xy)$ . One can verify that this satisfies the definition of an inner product. Then we have

(3) $\begin{align*} \vert E(xy)\vert &=\vert \left<x,y\right>\vert\\ &\leq \Vert x\Vert \cdot \Vert y\Vert\textrm{ by Analysis CS}\\ &= \sqrt{\left<x,x\right>}\sqrt{\left<y,y\right>}\\ &=\sqrt{E(x^2)}\sqrt{E(y^2)} \end{align*}$

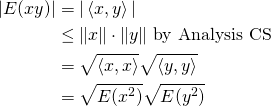
it seems so obvious but I’d never realized this previously. Further, the statement

(4) $\begin{align*} \vert Cov(x,y)\vert &\leq \sqrt{Var(x)}\sqrt{Var(y)} \end{align*}$

becomes really easy to prove using the inner product defined above.

(5) $\begin{align*} \vert Cov(x,y)\vert &=\left<x-E(x),y-E(y)\right>\\ &\leq \sqrt{\left<x-E(x),x-E(x)\right>}\sqrt{\left<y-E(y),y-E(y)\right>}\textrm{ by CS}\\ &=\sqrt{Var(x)}\sqrt{Var(y)} \end{align*}$

Related Posts

Leave a Reply Cancel reply