Solving Full Rank Linear Least Squares Without Matrix Inversion in Python and Numpy

In this post we describe how to solve the full rank least squares problem without inverting a matrix, as inverting a matrix is subject to numerical stability issues. We first describe the least squares problem and the normal equations, then describe the naive solution involving matrix inversion and describe its problems. We then describe two other methods: the Cholesky decomposition and the QR decomposition using householder matrices. The first is also unstable, while the second is far more stable. We show examples in python, using numpy and scipy.

The Least Squares Problem

Let $A\in \mathbb{R}^{m\times n}, x\in \mathbb{R}^n,b\in \mathbb{R}^m$ , and let $A^TA$ be full rank. The least squares problem is to solve

(1) $\begin{align*}\min_x\Vert Ax-b\Vert_2\end{align*}$

the main application of this is in linear regression, although in that setting it’s generally written as

(2) $\begin{align*}\arg\min_x\Vert X\beta-y\Vert_2\end{align*}$

we will use the former notation, which is common in the numerical linear algebra literature.

Normal Equations

In order to solve this, we can expand the terms in the norm and take derivatives, giving us the normal equations:

(3) $\begin{align*}A^T Ax&=A^Tb\end{align*}$

the simplest way to solve this is to compute $(A^T A)^{-1}$ and then compute

(4) $\begin{align*}x=(A^T A)^{-1}A^Tb\end{align*}$

however let $0\leq \sigma_1\leq \cdots \sigma_n$ be the singular values of $A^TA$ . If $\frac{\sigma_1}{\sigma_n}$ is close to $0$ , then the computation of $(A^TA)^{-1}$ will have large errors. Let’s try an extreme case where the matrix $A$ is almost singular, and the number of rows is equal to the number of columns.

import numpy as np
from scipy import linalg

np.random.seed(3)
m = 1000
n = 1000
Cov = 0.999999*np.ones((n,n))
np.fill_diagonal(Cov,1)
A = np.random.multivariate_normal(np.zeros(n),Cov,m)
b = np.random.normal(0,1,m)
gram = np.dot(A.T,A)
print(np.linalg.cond(gram))

6.392675702631713e+17

this has extremely high condition number, suggesting that many procedures, in particular matrix inversion, will be numerically unstable. Let’s try solving the least squares problem and computing the residual norm $\Vert r\Vert_2=\Vert A^TA\hat{x}-A^Tb\Vert_2$ for our estimate $\hat{x}$ .

x_normal_equations = np.dot(np.linalg.inv(gram),np.dot(A.T,b))
r_norm = np.linalg.norm(np.dot(gram,x_normal_equations)-np.dot(A.T,b))
print(r_norm)

35.13589871545292

this is a huge error! Clearly we can’t use this method as an all purpose solution.

Cholesky Decomposition

One alternative to inverting the matrix is to do a Cholesky decomposition $AA^T=LL^T$ , where $L$ is lower triangular. We can then solve

(5) $\begin{align*}LL^Tx&=A^Tb\end{align*}$

we can then solve the triangular system $Ly=A^Tb$ for $y$ and $L^Tx=y$ for $x$ . Let’s see how this does.

gram = np.matrix(gram)
L = np.linalg.cholesky(gram)
y = linalg.solve_triangular(L,A.T.dot(b),lower=True)
x_cholesky = linalg.solve_triangular(L.T,y)
r_norm_cholesky = np.linalg.norm(np.dot(gram,x_cholesky)-np.dot(A.T,b))
print(r_norm)

35.13589871545292

this is the same error. Clearly we can’t use this either.

Householder QR

Householder QR finds a sequence of householder matrices $H_1,\cdots,H_k$ such that $H_k\cdots H_1A=R$ , where $R$ is upper triangular, and $H_1,\cdotsH_k=Q$ , where $Q$ is an orthogonal matrix. Thus $A=QR$ is a $QR$ decomposition. This is more stable than a QR decomposition using classical gram schmidt.

We can plug this into the normal equations via

(6) $\begin{align*}A^TAx&=A^Tb\\R^TQ^TQRx&=R^TQ^Tb\\R^TRx&=R^TQ^Tb\\Rx&=Q^Tb\end{align*}$

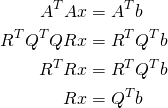
we can then solve the triangular system $Rx&=Q^Tb$ for $x$ .

Q,R=np.linalg.qr(A)
x_householder=linalg.solve_triangular(R,Q.T.dot(b))
r_norm_householder = np.linalg.norm(np.dot(gram,x_householder)-np.dot(A.T,b))
print(r_norm_householder)

5.681399611646504e-05

This is far more stable!

Discussion

In this post we describe three methods for solving the normal equations for full rank $A^TA$ . The first two are particularly vulnerable to numerical errors, while the third is more robust.

The Least Squares Problem

Normal Equations

Cholesky Decomposition

Householder QR

Discussion

Related Posts

Leave a Reply Cancel reply