Here we’ll talk about multicollinearity in linear regression.
This occurs when there is correlation among features, and causes the learned model to have very high variance. Consider for example predicting housing prices. If you have two features: number of bedrooms and size of the house in square feet, these are likely to be correlated. Consider a correctly specified model for linear regression. The mean squared error in the learned model ![]() can be decomposed into squared bias and variance. If we estimate
can be decomposed into squared bias and variance. If we estimate ![]() via ordinary least squares (OLS), the bias is
via ordinary least squares (OLS), the bias is ![]() , so that
, so that
(1) ![Rendered by QuickLaTeX.com \begin{align*} \mathbb{E}((\hat{\beta}-\beta)^T(\hat{\beta}-\beta)|\boldsymbol{X})&=\textrm{Var}(\hat{\beta}|\boldsymbol{X})\\ &=\sigma^2 \Tr[(\boldsymbol{X}^T \boldsymbol{X})^{-1}] \end{align*}](https://boostedml.com/wp-content/ql-cache/quicklatex.com-ea07d4510e6bffb379872366249838a0_l3.png)
Let’s investigate the effect of multicollinearity by looking at parameter learning accuracy under both multicollinear features and independent features. We will first look at empirical performance and then talk about the theory of why we see this. We will use the following linear model
![]() where
where ![]() i.i.d. and
i.i.d. and ![]() . For multicollinear data we use
. For multicollinear data we use
(2) 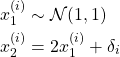
Thus the two features have some amount of multi-collinearity, but the gram matrix ![]() is still invertible. For independent data we use
is still invertible. For independent data we use
(3) 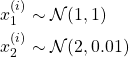
We now sample 200 ![]() pairs of both multicollinear and independent data and perform OLS. We repeat this 30 times and plot density estimates of the learned parameters.
pairs of both multicollinear and independent data and perform OLS. We repeat this 30 times and plot density estimates of the learned parameters.
As we can see, the variance with multicollinear features is drastically higher. In particular, with independent features we generally get a pretty good learned model, whereas with multicollinear features, some of the learned models are useless. Why is this? Recall that for a given dataset,
(4) ![]()
Now with multicollinearity, ![]() will have “almost” linearly dependent columns, leading to some eigenvalues being very small. Now
will have “almost” linearly dependent columns, leading to some eigenvalues being very small. Now
(5) 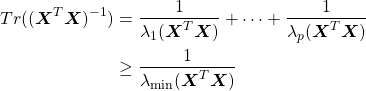
where ![]() is the
is the ![]() th eigen-value. Thus having a single small eigenvalue will lead to very large mean squared parameter error. Let’s see what the smallest eigenvalues look like in practice under both the multicollinear and independent data.
th eigen-value. Thus having a single small eigenvalue will lead to very large mean squared parameter error. Let’s see what the smallest eigenvalues look like in practice under both the multicollinear and independent data.
As expected, the min eigenvalues are much smaller under multicollinearity. To sum up:
- Multicollinearity is when features are correlated
- It leads to high variance in the learned model.
- The reason for this is that the the min eigenvalues of the Gram matrix of the features becomes very small when we have multicollinearity.
In the future, we will discuss how to detect multicollinearity and what to do about it.